The appearance and reemergence of infectious diseases are continuously documented in the history of mankind with the design of their transmissions, being strongly related to economic globalization, environmental, demographic and technological changes.

Some infectious agents caused countless deaths before they disappeared; others became endemic (periodic epidemics) in a population and, consequently, traced a profile of inequalities, highlighting poor regions and with precarious health systems.

Pathologies such as malaria, cholera, schistosomiasis, tuberculosis, arboviruses in general (diseases transmitted by vectors such as mosquitoes), respiratory problems, among others, have a significantly negative impact on the life expectancy of the population, and affect the economy of a country, since a sick population has a reduced workforce.

In this scenario, modeling has become an ally, contributing to the understanding of the complexities of the transmission and evolution of pathogens, prediction of trends and their control.

They are models that harmonize with different contexts, capture individual characteristics up to a macro level - taking into account regional, social and economic characteristics of the population.

The results obtained guide the areas of epidemiology and public health in the study of the dynamics of transmission and control of contagion of infectious diseases.

by ARTHUR RIOS, JULIANE OLIVEIRA, MORENO RODRIGUES, PABLO RAMOS

Despite the modern definition of IDs, the existence of microorganisms was only demonstrated in the 17th century by scientist Van Leeuwenhoek, arising from the appearance of the first microscope. Still without the creation and formalization of the theory microbial disease, one of the first contributions of modeling came from the work of John Graunt (merchant, also considered one of the first demographics and epidemiologists in history, 1620 - 1674) in his book Natural and Political Observations made upon the bills of Mortality , in 1662, based on data on IDs and mortality [4] .

From the analysis of his data, the author provided a method to study the hypothesis of which risk factors caused by infections of various diseases compete for the live of the individuals (in other words, for each individual, one of these risks 'will win', and the individual will die because of that risk). His ideas initiated the competitive risk theory that goes beyond the causes of illness-motivated deaths. Since then, only at the end of the 19th century and the beginning of century, we have a better understanding of the agents that cause infectious diseases with the principle of microbial theory of diseases, described by Jacob Henle (doctor, pathologist and anatomist, 1809 - 1885), in 1840, and which was developed by Robert Koch (physician and microbiologist, 1843 - 1910), Joseph Lister (surgeon, 1827 - 1912) and Louis Pasteur (biologist, microbiologist and chemist, 1822 - 1875).

Until the end of the 20th century, IDs were responsible for a large part of the mortality rate and malformations in the population. Global pandemics like smallpox, cholera and flu have periodically threatened the survival of entire populations. With the improvement of sanitary conditions, water supply and changes in the population's quality of life, IDs have given rise to non-infectious diseases, which are responsible today for most of the causes of death in the world [2 , 3] .

In fact, the smallpox epidemy was one of the worst diseases in human history, being also the only disease in the world to be eradicated and one of the world's most triumphant achievements in medicine [5] . Coincidentally, the first model associated with mathematical epidemiology was added to the work of Daniel Bernoulli (mathematician and physicist, 1700 - 1782) [6] . In 1760, Bernoulli wrote an article entitled "An attempt at a new analysis of the mortality caused by smallpox and of the advantages of inoculation to prevent it" [6 , 7] .

In the absence of a vaccine, Bernoulli's work aimed to understand whether inoculation (the voluntary introduction of a small amount of less virulent smallpox into the body to protect it from further infections) would be a technique to be considered, even if it was sometimes a deadly operation. Using data on smallpox cases from Halley's Mortality Table and mathematical modeling, Bernoulli estimated that inoculation could be advantageous if the risk factors associated with death were less than 11% and, consequently, inoculation could increase life expectancy at birth by 3 years.

Another notable contribution from IDs modeling is related to the cholera epidemic. Cholera had a major impact in the 19th century, being significantly reduced in developed countries due to improved sanitation and water treatment. However, the disease is still endemic in more than 47 countries worldwide, causing approximately 2.9 million cases and killing about 95,000 people. [8] In the epidemy of 1855 in London, the physician John Snow (1813 - 1858) contributed to the discovery of the causal source of the cholera epidemy in the city [9] . To do this, Snow developed a study to analyze space-time patterns of cholera cases during the epidemy, thus obtaining the location of a source of water supply responsible for infections.

The previous examples were striking points in the history of infectious diseases, giving a summary of what was developed at the beginning of the modeling of IDs. However, contributions in the area of ​​ID modeling occurred mostly from the 20th century, having nowadays separate research branches in statistics, mathematics and computational modeling. These areas intersect with the concept of model, which can be traced in several ways, having different levels of complexity, with different study objectives, depending on the data evaluability, computational resources, precision and generality required and the time window available for the demand of results. However, also, we cannot forget, consistent with the definition of the word, a “Model” is a representation, imitation and, therefore, does not have the power to faithfully describe a natural phenomenon. Therefore, a model always it will be accompanied by hypotheses that correspond to the conditions put in place and facilitate and enable its mathematical-statistical and computational manipulation.

The three areas communicate and are based on epidemiological foundations, thus creating an interdisciplinary niche, which develops theories and applications that have immediate effects on populations.

References

[1] Barreto ML, Teixeira MG, Carmo EH. Infectious diseases epidemiology. Journal of Epidemiology Community Health. Mar 1;60(3):192-5, 2006.

[2] Saker, L., Lee, K., Cannito, B., Gilmore, A., Campbell-Lendrum, D. H. Globalization and infectious diseases: a review of the linkages. (No. TDR/STR/SEB/ST/04.2). World Health Organization, 2004.

[3] Holmes, King K., Stefano Bertozzi, Barry R. Bloom, Prabhat Jha, Hellen Gelband, Lisa M. DeMaria, and Susan Horton. Major infectious diseases: key messages from disease control priorities. 2017.

[4] Smith, David and Keyfitz, Nathan. Mathematical demography: selected papers. Springer Science & Business Media, Vol. 6., 2012.

[5] Fenner, Frank, Donald Ainslie Henderson, Isao Arita, Zdenek Jezek, and Ivan D. Ladnyi. Smallpox and its eradication. Vol. 6. Geneva: World Health Organization, 1988.

[6] Bacaër, Nicolas. Daniel Bernoulli, d’Alembert and the inoculation of smallpox (1760). In A short history of mathematical population dynamics, pp. 21-30. Springer, London, 2011.

[7] Bernoulli, Daniel, and Sally Blower. An attempt at a new analysis of the mortality caused by smallpox and of the advantages of inoculation to prevent it. Reviews in medical virology 14, no. 5:275, 2004.

[8] WHO. Cholera: The Forgotten Pandemic. https://www.who.int/cholera/the-forgotten-pandemic/en/, 2018.

[9] Snow, John. On the mode of communication of cholera. John Churchill, 1855.

by NATÁLIA TAVARES

The inoculation strategy is similar to natural immunity strategies because it considers exposure to the infectious agent as a preventive method for the disease in question. However, both are strategies that are at risk of developing the disease in its severe form and progressing to death. Therefore, risk assessment is crucial to estimate the potential advantages and disadvantages of these strategies, both at the individual and population levels.

Unlike what happens with a vaccine, where the inoculum is composed only of parts of the microorganism or a non-infectious vector, generating immunity without disease, in the inoculation strategies or natural immunity, individual responses are unknown and the risks of evolution to a severe form is considerable.

Therefore, it is important to consider that the term “collective immunity” defines a resistance to the spread of a contagious disease in a given population. This is because a significant portion of the population is immune to the microorganism, reducing the chances of transmission between an infected individual to another susceptible [1] . In other words, immunized individuals buid a containment barrier, protecting non-immunized individuals.

However, collective immunity is based on individual immunity. Once an individual is exposed to an exogenous substance or infectious agent, responds to these stimuli and eliminate them to maintain his healthy state, he is considered immune. In addition, immunity can be induced by vaccination. In this way, collective immunity can be achieved through vaccination or by many people being infected by the infectious agent.

Collective immunity was already observed for measles in the USA in the 1930s, where outbreaks were contained after 68% of children were infected [2] . This continued for the following decades, with low case numbers until the vaccine was introduced in the 1970s [3] .

There are also some relevant examples of infectious diseases that have been eradicated or had their spread controlled through collective immunity. Smallpox, for example, was officially declared eradicated in 1979 on the basis of collective immunity achieved through intense vaccination campaigns (Lane, 2006). Although diseases such as measles, rubella and whooping cough have not yet been eradicated, collective immunity is maintained through the high proportions of immune individuals that protect those susceptible [4] .

In the case of Covid-19, where there is no approved vaccine, collective immunity cannot be achieved through vaccination. In this sense, collective immunity would be achieved through natural infection. So, what would be the proportion of people who need to be immunized against Covid-19 to generate a barrier to contain and protect the non-immunized?

There are different methods of projecting these numbers, but on average, estimates indicate that about 56% of the population would need to be immune to achieve collective immunity against Covid-19. However, it is important to consider the possible outcomes and risks that result from natural infection or inoculation. An individual naturally infected with SARS-CoV-2 may recover from the disease or may die due to the evolution to the severe form of the disease.

According to epidemiological data, Covid-19 manifests itself with severe cases in approximately 15% of infected individuals with an average mortality rate of 2%. Considering these values, it is important to consider the “costs” that the natural infection can bring. These “costs” involve since loss of life due to the severe form of the disease, as well as burdening the health systems that manage the care of these patients. Therefore, mathematical modeling has been fundamental for the development of studies that assess the risks arising from collective immunity achieved through natural infection or inoculation.

About the author

Natália Machado Tavares has a degree in Biological Sciences (UFBA, 2005), a master's degree (UFBA-FIOCRUZ/BA, 2008) and a PhD (UFBA-FIOCRUZ/BA, 2013) in Experimental Pathology. She participated in the team coordinated by Dr. Nicolas Glaichenhaus in the PhD intership (Scholarship CNPq-SWE, 2012) in the area of ​​Mucosal Immunity and Inflammation (IPMC-Université de Nice/France). She did postdoctoral studies at CPqGM-FIOCRUZ/BA, investigating the interaction between dendritic cells and human neutrophils in cutaneous leishmaniasis. She also participated in the team coordinated by Dr. Carlos Henrique Serezani during postdoctoral studies at Indiana University-Purdue University of Indiana (Indianapolis, USA). Currently she is a Researcher at the Gonçalo Moniz Institute (FIOCRUZ-BA), working on topics related to immunology, cellular, molecular biology, parasitology and global data analysis, with emphasis on the role of innate immunity. She has developed projects on the themes: microRNAs expressed in skin diseases, comorbidities in human Leishmaniasis and receptors for activation of innate immunity.

Curriculum

References

[1] Smith, David R. Herd Immunity. The Veterinary clinics of North America. Food animal practice 35, no. 3:593-604, 2019.

[2] Fine, Paul EM. Herd immunity: history, theory, practice. Epidemiologic reviews 15, no. 2:265-302, 1993.

[3] McNabb, S. J., R. A. Jajosky, P. A. Hall-Baker, D. A. Adams, P. Sharp, W. J. Anderson, A. J. Javier et al. Summary of notifiable diseases—United States, 2005. MMWR. Morbidity and mortality weekly report 54, no. 53:1, 2007.

[4] Fine, Paul, Ken Eames, and David L. Heymann. Herd immunity: a rough guide. Clinical infectious diseases 52, no. 7:911-916, 2011.

by JULIANE OLIVEIRA

The mathematical modeling of infectious diseases (IDs) began in the late 19th century, when part of the studies presented was developed by public health professionals [1] . Until then, several questions were unanswered: what is the potential for an infectious agent to cause an epidemy? What is the proportion and duration of the epidemy? Will the disease affect the entire population? Can it disappear? Reappear? Become periodic? How will the spread of the disease behave in different settings?

To understand how the search for answers to the questions above developed, we can observe in the work of the physician Pyotr Dimitrievich EN’KO (1844 - 1916) a discussion that directed to the fundamentals of modeling a epidemy. EN’KO initially simplified the problem, considering that in a population we can have susceptible individuals, meaning, who can become infected when exposed to an infectious agent, as well as the possibility that part of that population is immune, in this case he assumed that the individual would never contract the disease.

Once the infected person enters this population, it will consequently get in contact with a healthy individual. If he/she is susceptible, he/she gets infected and becomes a transmitter of the disease. In his 1889 work [2] , EN'KO argues that the basic elements for describing the disease transmission process depend on the likelihood that a healthy person will come into contact with an infected person, the likelihood that he or she will become infected and the number of susceptible people in the population. Thus, small and isolated communities make it difficult to transmit a disease; otherwise, large societies, and in particular with a high rate of contact between individuals, are more likely to have epidemics.

In 1906, the physician and epidemiologist William Heaton Hamer (1862-1936) argued that the spread of a disease depends on the number of susceptible and infected individuals, thus recognizing that only the decrease in the density of susceptible people could stop an epidemic. To describe the rate of new infections in a population, Hamer suggested using the Law of Mass Action: a proposition that states that the rate of the chemical reaction is directly proportional to the product of the interactions or concentrations of the reagents, thus making an analogy between "rate of chemical reaction" and "rate of new infections" [3] .

This was the first step that enabled the formalism of disease transmission through mathematical equations, giving rise to compartment models. A compartment is a schematic grouping of the population where they are divided in groups of individuals with similar characteristics. When these characteristics are related to an infectious disease, the simplest example of dividing the study population is between three compartments:

• susceptible individuals (S),
• infected individuals (I),
• immunized individuals (R).

In 1902, Ross was awarded the Nobel Prize in Medicine for his work that described the dynamics of malaria transmission between mosquitoes and humans. Ross showed that by reducing the mosquito population to a certain level, it would be possible to eliminate malaria transmission, thus giving the first concept of the basic reproduction number [4] .

Up to the current date, given their simplicity, compartmental models form the basis for the conceptual construction of infectious disease modeling. In order to build such a model, the first step is to understand the biological phenomenon you want to study (model): what type of disease do you want to model? How is it transmitted?

If there are factors that influence its transmission, such as age, climate, social conditions etc; subsequently, to translate the biological, behavioral, immunological and demographic aspects in terms that allow us to analyze the phenomenon with mathematical rigor, technically described by equations.

Mathematical equations will subsequently be calibrated with available data, in other words, measurements and observations of the phenomenon. Finally, since the conditions of analysis are biologically and mathematically plausible, we draw the conclusions, interpreting the mathematical language in biological terms. Once the model is validated, it is possible to simulate scenarios that direct public policy measures that contribute to the control and even elimination of a disease in the population.

Currently, with the spread of SARS-COV-2, the causal agent of Covid-19, and in the absence of a vaccine, several models are being constructed to describe the evolution of the disease in different social contexts. At the beginning of the epidemic, simple models such as SIR (Susceptible- Infected- Recovered) or even SEIR (E refers to Exposed) are adequate to analyze the potential for spreading the disease in the region.

In order to target measures to control the disease, compartments that simulate quarantines and isolation of infected individuals can be added to the previous models, thus giving an idea of ​​the impact of these measures on the flattening of the infected curve. In more critical scenarios, in which the application of more restrictive measures becomes unfeasible, strategies to protect the health system can be considered when adding hospital dynamics to the model [5 , 6 , 7] .

These are some of the various modeling techniques that have been and are being developed to contain the dissemination of Covid-19, generating themes beyond the objective of this Newsletter.

References

[1] Foppa, Ivo M. A Historical Introduction to Mathematical Modeling of Infectious Diseases: Seminal Papers in Epidemiology. Academic Press, 2016.

[2] En’ko, P.D. (1889). On the course of epidemics of some infectious diseases. Vrach. St. Petersburg, X, 1008-10010, 1039-1042, 1061-1063 (in Russian). English translation by Dietz, K. International Journal of Epidemiology 18, 749-755, 1989.

[3] Hamer, William Heaton. The Milroy lectures on epidemic disease in England; the evidence of variability and of persistency of type. https://archive.org/details/milroylectureson00hameuoft/page/26/mode/2up,1906.

[4] Ross, Sir Ronald. Memoirs with a full account of The Great Malaria Problem and its Solution. Albemarle Street, W. London: John Murray. p. https://archive.org/details/b29825738/page/n13/mode/2up, 1923.

[5] Amad, Alan, Aureliano Sancho Souza Paiva, Caio Porto de Castro, Daniel Cardoso Pereira Jorge, Diego Santos Souza, Elaine Cristina Cambui Barbosa, Gabriel Bertolino et al. Boletim Covida – Acompanhamento da pandemia por Covid-19 no Brasil: destaque para a situação na Bahia. https://redecovida.org/relatorios/boletim-covida/, 2020.

[6] Amad, Alan, Aureliano Sancho Souza Paiva, Caio Porto de Castro, Daniel Cardoso Pereira Jorge, Diego Santos Souza, Elaine Cristina Cambui Barbosa, Gabriel Bertolino et al. Boletim Covida – Pandemia de Covid-19. https://redecovida.org/relatorios/boletim-covida-ed-02/, 2020.

[7] Amad, Alan, Aureliano Sancho Souza Paiva, Caio Porto de Castro, Daniel Cardoso Pereira Jorge, Diego Santos Souza, Elaine Cristina Cambui Barbosa, Gabriel Bertolino et al. Boletim Covida: Pandemia de Covid-19: fortalecer o Sistema de Saúde para proteger a população. https://www.arca.fiocruz.br/bitstream/icict/41472/2/boletim_4_rede_covida_final.pdf , 2020.

by NIVEA SILVA and ROSEMEIRE FIACCONE

“Statistics” is a word derived from the Latin status, originally means “the study of the state”. Its history begins with the ancient Egyptians, around the year 5000 before the Christian era, who already at that time maintained a system of registration of their prisoners of war, and with the Chinese, who were the first around the year 2000 before the era Christian to worry about population growth, conducting a census of its population and cultivated crops.

In the Christian Era, the creation of the first crossed statistical tables is assigned to the mathematician and astronomer Menelaus of Alexandria and the Constantines owned the first Statistics agency. The Arabs, around the 695s, used the idea of ​​weighted average to count coins and, in 826, used statistical calculations as a strategy to take Crete * .

It was the German academic Gottfried Achenwall, considered one of the fathers of Statistics, one of the first to introduce, in the 17th century, the term “Statistics” and use it to analyze economic, social and political information. Thus, the first applications of statistical thinking were, at the time, focused on the formulation of public policies, providing demographic and economic data.

Still in the 17th century, mathematicians Blaise Pascal and Pierre de Fermat also studied statistics, through the development of probability theory, to solve problems related to games of chance. One of the most important theorems in the area of ​​probability, known as the Law of Large Numbers (LGN), was formulated in the 18th century by the Swiss mathematician Jacob Bernoulli. This and other contributions by Jabob were published a few years after his death in the book Ars Conjectand, edited by his nephew Nicholas Bernoulli.

Another important contribution of this century, which has revolutionized Statistics today, is attributed to the English Presbyterian mathematician and pastor Thomas Bayes. Reverend Bayes, as he was known, demonstrated the famous theorem that bears his name: the Bayes theorem. This and other results attributed to Bayes were brought together in an essay called "Essay Towards Solving a Problem in the Doctrine of Chances", published in 1763, after his death, in the Philosophical Transactions of the Royal Society of London. The reasoning constructed by Bayes on this theorem gave rise, years later, to a new paradigm in Statistics: the Bayesian paradigm.

It was, however, from the 19th century, through the contributions of names such as:

• the French mathematician, astronomer and physicist Pierre-Simon de Laplace (inverse probability principle, central Moivre-Laplace limit theorem, among others),
• the mathematician and German physicist Carl Friedrich Gauss (least squares method),
• by English anthropologist, meteorologist, mathematician and statistician Francis Galton (Theory of regression, initial notion of correlation, demonstrated later by Pearson),
• by British statistician Karl Pearson (founder of Biometrika journal , demonstrated the correlation coefficient and was one of the first to affirm that correlation does not imply causality; he proposed the chi-square test and method of moments, among other contributions),
• of the British statistician, evolutionary biologist and geneticist Ronald Fisher (proposed the Likelihood, function that plays a central role in Statistics, producing theoretical results of information statistical difference ranging from parameter estimation, using the maximum likelihood method, to the performance of hypothesis tests and construction of regions of confidence. He also developed ANOVA and the area of ​​design of experiments),

In the first half of the 20th century, several inference results were demonstrated by Fisher and mathematicians such as Jerzy Neyman, Egon Pearson and Abraham Wald. In the same period, experimental designs and sample surveys were developed, as well as fundamental ideas about time series [1] . In the 1972s, Nelder and Wedderburn proposed the class of models known as generalized linear models (GLM), which in addition to including the normal linear model as a particular case, encompasses the logistic regression and Poisson models, in addition to the analysis models of variance and covariance, among others.

The importance of GLM's and the extensions proposed from this class goes beyond the different possibilities of application. As it constitutes an approach that unifies several statistical models, it also promotes the central role of verisimilitude in the theory of inference. In 1977, the well-known EM (Expectation Maximization) algorithm, commonly used to estimate the parameters of several statistical models, was proposed by Dempster and collaborators as a maximization strategy based on the idea of ​​missing data.

Before the 1990s, however, Monte Carlo-based methods [8] , such as Markov Monte Carlo (MCMC) chains, had not yet won strength in the statistical community and a possible justification is due to the lack of computational development at the time, although there is already a consolidated theory of algorithms based on Metropolis-Hastings and the Gibbs sampler [5] .

Since the 20th century, statistical methods have been developed, mixing logic, science and technology to solve and investigate problems in different areas of human knowledge [4] . One of these areas is Epidemiology, a branch of medicine that studies the different factors that intervene in the diffusion and propagation of diseases, and has, since the 17th century, a close relationship with Statistics, when the British scientist and demographer John Graunt, precursor in the construction of the mortality tables, he realized the importance of the quantitative analysis of the so-called vital events (births, deaths and fetal losses).

Graunt used data from an annual time series (from 1604 to 1660), collected in London parishes, and concluded, among other things, that most births were to male children, despite the distribution by sex being homogeneous in the population overall, that there were high mortality rates in the first years of life and that mortality was higher in urban areas compared to rural areas [1] .

In the 19th century, William Farr, considered the first statistical physician in the general records office in England and Wales, made use of the civil registry for the study of diseases and proposed a classification for the causes of death, which years later would serve as structural basis for the current international classification of diseases. It was, however, in the middle of the 20th century, with the consecration of the theory of multicausality (according to this theory, the cause of a given disease is not unique, meaning, in its appearance several causes coexist due to various causal factors), that epidemiologists began to adopt Statistics as an analytical methodology in their studies [6] .

Speaking specifically of infectious disease modeling, the increasing use of deterministic mathematical models for representing epidemics is notorious, as described in the previous sections. However, statistical (or stochastic) models have gained a lot of space in this area, due, among other factors, to the improvement of computational resources in the last two decades, in addition to the use and dissemination of estimation procedures based, for example, on MCMC methods.

Statistical tools for modeling infectious diseases can provide evidence, in terms of probability, whether an infection is spreading or being controlled in a population, whether infection rates vary according to important demographic factors, or whether certain health interventions or not are having the desired impact [7] . The approaches proposed in the literature range from the application of GLM's (or extensions of this class), the use of usual time series models, as well as their extensions for non-normal responses, to the use of spatial models for disease mapping, which consist, for example, finding spatial patterns (correlations) of the disease under study.

More recently, the pandemic caused by the new coronavirus has brought to light the importance of statistical and mathematical modeling within this scenario, and many applications based, for example, on logistic growth models, Poisson model with overdispersion, changepoint models, among others, have been proposed in an attempt to model the curve of new cases and/or deaths caused by Covid-19.

It is important to highlight that the existing methodologies in the literature for general statistical modeling and, in particular, the modeling of infectious diseases, have assumptions, in addition to positive and negative points, and such factors need to be taken into account in scientific research. It is worth mentioning that in the case of infectious diseases, the individual depends on other individuals around him to become infected and the transmitting vector is hardly known, meaning, by whom the person was infected, nor the exact time the subject became infectious. Thus, the quality and availability of information is fundamental for certain scientific hypotheses to be verified.

Finally, another important point is that appropriate data must be available for analysis, since without them, the hypotheses of interest may not be adequately tested.

About the authors

Nivea Bispo da Silva has a degree (UFBA, 2007) in Statistics, a Master's (UFMG, 2013) and a PhD (UFMG, 2017) in Statistics. Current adjunct professor A and researcher at the Statistics Department of the Federal University of Bahia. She is a collaborator in the Center for Data Integration and Knowledge for Health (CIDACS), part of the Oswaldo Cruz Foundation, developing research on the Coorte platform of 100 million Brazilians. She has over ten years of research experience in the area of ​​Probability and Statistics, with an emphasis on Applied Statistics. She works mainly with the following themes: Analysis of longitudinal data, Analysis of correlated data, Finite mixture models and Bayesian statistics.

Curriculum

Rosemeire Leovigildo Fiaccone has a bachelor's degree in statistics (UFBA, 1988), a master's degree in statistics (UNICAMP, 1998) and a PhD in Statistics - Lancaster University (2006). She is currently Associate Professor II and researcher at the Federal University of Bahia and a collaborator in the Center for Data Integration and Knowledge for Health (CIDACS), part of the Oswaldo Cruz Foundation, developing research on the Coorte platform of 100 million Brazilians. With over 30 years of career, she has experience in the area of ​​Probability and Statistics, with an emphasis on Biostatistics, working mainly on the following themes: analysis of longitudinal data, analysis of correlated categorized data and structural equation models.

Curriculum

References

[1] Memória, J. M. P. Breve história da Estatística. Embrapa - Informação Tecnológica, 2004.

[2] Stanton, J. Galton, Pearson, and the Peas. A Brief History of LiM. near Regression for Statistics Instructors. Journal of Statistics Education, vol 9, issue 3, 2001.

[3] Stigler, S. The Epic Story of Maximum Likelihood. Statistical Science, vol. 22, n 4, 2007.

[24] Stigler, S. M. The history of Statistics: The measurement of uncertainty before 1900. Harvard University Press, 1986.

[5] Brooks, S., Gelman, A., Jones, G. L., Meng, Xiao-Le M. Handbook of Markov Chain Monte Carlo. Chapman Hall/CRC press, 2011.

[6] Szwarcwald, C. L., Castilho, E. A. de. Os Caminhos da Estatística e suas incursões pela Epidemiologia. Cadernos de saúde pública, vol 8, p. 05-21, 1992.

[7] Grant, B., Ozanne, M. Statistical Models for Infectious Diseases: A Useful Tool for Practical Decision-Making. American Journal of Tropical Medicine and Hygiene, vol 10, issue, 2019.

[8] Metropolis, N., Ulam, S. The Monte Carlo Method. Journal of the American Statistical Association. v. 44, n. 247, p. 335-41, Sep. 1949.

by ROBESPIERRE PITA and DANIELA ALMEIDA

The simplest definition for the term "computational modeling" corresponds to the description of a phenomenon using a programming language [1] . In this way, the effort to create a computational model involves observing a portion of the real world, describing the interactions between its different components and trying to express them in data and operations that can be used by a computer.

Let's take a simple example. Suppose you want to develop a penalty kick simulator. Thus, you know that you will need to take into account several characteristics for each kick (gravity, force and direction of the wind, model and material of the soccer cleats, size and weight of the ball, force of the kick, etc.) and that several mathematical models must be used to simulate each scenario well according to the intentions of the player and goalkeeper. It is very likely that these models are too complex to allow a readable or fast analytical solution, and, therefore, deriving your steps in computational operations and arranging your variables in data structures is perhaps the only way to build your simulator.

The writing of this program should guarantee behaviors of direction and effect of the ball that correspond to the player's commands and a result that also depends on the goalkeeper's commands, not to mention that the quality and acceptance of this program are very associated with the mathematical modeling used to reproduce the laws of physics on every kick. It is important to note that the relationship between mathematical and computational modeling is even broader and deeper than that shown in this example.

With an absurd complexity and volume of calculations necessary for the construction of nuclear bombs in the Manhattan Project, mathematician John von Neumann participated in the creation of Electronic Numerical Integrator and Computer (ENIAC) in 1944, the first electronic computer which included components similar to today's computers in its architecture: a memory unit, a processing unit and input and output peripherals [2] .

John von Neumann, in 1945, was also involved in the design of the first computer that ran programs previously stored in memory, the Electronic Discrete Variable Automatic Computer (EDVAC). This second project was heavily influenced by the universal Turing machine, proposed by Alan Turing in 1936. Turing was the mathematician and cryptanalyst responsible for creating a computer capable of decrypting the coded messages that were exchanged by the Nazis during the second world war through the Enigma Machine. Today, Alan Turing is considered the father of Computer Science.

This brief history should be enough for us to understand how close computational modeling is to mathematics since its genesis. Realize that even the architectures of classic computers were designed to serve the purposes of mathematical modeling. Since then, computer modeling has become a very relevant area of ​​knowledge, especially in solving complex nonlinear problems.

Today, computer scientists refine and apply the fundamentals of their field to try to answer several scientific questions that will contribute to our knowledge of the relationships between real-world phenomena - such as natural or social. The effectiveness of these models is greater mainly in contexts where there are mathematical structures capable of allowing abstraction, generalization and interpretation [1] , however, they are not dependent on these structures. The studies that most attract interests today are inserted in the context of Data Science and Big Data, themes that drive the evolution of computational modeling to deal with increasingly larger and more complex data structures.

The contribution of computer science to these topics further reinforces the importance of this epistemology and transcends the applications of its discoveries. It is not difficult to find practical examples from these studies in our daily lives: research aimed at understanding the relevance or popularity in a social network [3] , chat robots capable of being confused with real people [4 , 5] , facial recognition [6] , among others.

The advent of Data Science has further boosted the use of machine learning to solve everyday issues - task automation, event prediction, diagnostics, etc. - and there's a lot of collaboration from computer science in that.

Machine Learning is a branch of Artificial Intelligence. Any program that improves performance in performing a given task can be classified as a computer model of machine learning while its experience increases. This experience can be characterized by greater training data. Consider as a practical example a program capable of playing cards that wins more according to the number of games it plays.

Although the foundations of these programs are based on mathematics and statistics, computational modeling has two essential collaborations. The first is the implementation of increasingly optimized and scalable programs, in other words, with reduced execution time or capable of handling large amounts of data on multiple processors or computers. The second is the idealization and implementation of innovative and increasingly complex computational models, such as Deep Learning.

Deep Learning models simulate the functioning of our brain cells, assembling deep neural networks, arranged in hierarchically interconnected layers that lead the input data to several derivations to allow the prediction of future events or the grouping of current data. It is common to use these techniques for speech analysis, speech recognition and visual recognition, for example.

It would not be surprising that, like the mathematical, statistical and health sciences, computer models could be used to actively contribute to the understanding and monitoring of the new coronavirus (SarsCoV-2) pandemic.

Tens of thousands of scientific articles have made public the efforts of several computer scientists who, in collaboration with mathematics, statistics and health researchers, have focused on issues related to the state of emergency caused by the pandemic to gain knowledge about its dynamics and save lives. In response to the limitations of mass diagnosis for monitoring the infected, the mastery and use of machine learning techniques allowed clinical data to be used to predict who might be sick even without presenting any symptoms [7 , 8] . The lack of tests also drove Deep Neural Networks to be set up to support diagnosis through pattern recognition in lung imaging [9] . Or, to avoid further pressure on the health system, Deep Learning models were used to predict the risk of a patient needing to be admitted to a infirmary or ICU [10] . Many other initiatives are being published at every moment, there are even potential collaborations in the race for the vaccine [11] .

The potential of computer science in modeling infectious diseases is enormous. The advances in techniques used in monitoring and responding to everyday events, especially during a pandemic, are also considerable. The collaborations and networking of researchers from the most diverse areas of knowledge, however, were fundamental to leverage knowledge and reduce our limitations. It is of utmost importance to emphasize that there is still a lot to understand and that many other issues on this same topic may surface, bringing even greater challenges. We need to be ready to face ignorance with even more knowledge.

About the authors

Robespierre Dantas da Rocha Pita has a Bachelor's Degree (Universidade Salvador, 2010) in Information Systems, a Master's (UFBA, 2015) and a PhD (UFBA, 2019) in Computer Science. He is a specialist in Computer Networks and substitute professor and guest at the Federal University of Bahia, National Service of Industrial Learning of Bahia, Faculdade Maurício de Nassau and at the University of Salvador. He is currently a researcher at the Data Integration and Knowledge Center for Health (CIDACS) part of the Oswaldo Cruz Foundation, working in the areas of Distributed Systems, Machine Learning and Data Science, with particular emphasis in the area of ​​Computing Applied to Health.

Curriculum

Daniela Santos Almeida has a degree in Internet Systems from Universidade Salvador - UNIFACS (2016). Almeida was awarded a Diploma of Honor to Merit due to her academic performance of excellence in 2017 and twice obtained the Academic Merit Award in 2014 and 2015 at UNIFACS. She has already produced research and technologies on the Coorte platform of 100 million Brazilians and on the long-term surveillance platform for Zika, at the Center for Data Integration and Knowledge for Health (CIDACS) part of the Oswaldo Cruz Foundation. She is currently a Master's student in Computer Science at the Federal University of Bahia, developing research on Natural Language Processing, and is also in the process of specializing in Big Data and Business Intelligence. She is a Senior Data Engineer at Magnetis Gestora de Investimentos. She has experience in Computer Science, with an emphasis on Engineering and Data Science.

References

[1] Mahoney, MS Historical perspectives on models and modeling. XIIIth DHS-DLMPS joint conference on “scientific models: Their historical and philosophical relevance, 2000.

[2] Stallings, William Arquitetura e Organização de Computadores 8a Edição. Prentice-Hall, Pearson, 2010.

[3] Gabardo, Ademir C Análise de redes sociais: uma visão computacional. Novatec Editora, 2015.

[4] Kuyven, Neiva Larisane and Antunes, Carlos André and de Barros Vanzin, Vinicius João and da Silva, João Luis Tavares and Krassmann, Aliane Loureiro and Tarouco, Liane Margarida Rockenbach. Chatbots na educação: uma Revisão Sistemática da Literatura. RENOTE-Revista Novas Tecnologias na Educação, 16, 1, 2018.

[5] Maeda, A and Moraes, S. Chatbot baseado em deep learning: um estudo para língua portuguesa. Symposium on Knowledge Discovery, Mining and Learning, 5th, 2017.

[6] Dubey, Arun Kumar and Jain, Vanita. A review of face recognition methods using deep learning network. Journal of Information and Optimization Sciences, Taylor & Francis, 40, 2, 547–558, 2019.

[7] Banerjee, Abhirup and Ray, Surajit and Vorselaars, Bart and Kitson, Joanne and Mamalakis, Michail and Weeks, Simonne and Baker, Mark and Mackenzie, Louise S. Use of machine learning and artificial intelligence to predict SARS-CoV-2 infection from full blood counts in a population. International immunopharmacology, 86, 106705, Elsevier, 2020.

[8] Batista, AF d M and Miraglia, JL and Donato, THR and Chiavegatto Filho, ADP and de Moraes Batista, André Filipe and Miraglia, João Luiz and Donato, Thiago Henrique Rizzi and Chiavegatto Filho, Alexandre Dias Porto. Covid-19 diagnosis prediction in emergency care patients: a machine learning approach. Hospital Israelita Albert Einstein-Big Data Analytics M, São Paulo, SP, Brazil., Department of Epidemiology SoPH, University of Sao Paulo, Sao Paulo, Brazil, editors, 2020.

[9] Harmon, Stephanie A and Sanford, Thomas H and Xu, Sheng and Turkbey, Evrim B and Roth, Holger and Xu, Ziyue and Yang, Dong and Myronenko, Andriy and Anderson, Victoria and Amalou, Amel and others. Artificial intelligence for the detection of Covid-19 pneumonia on chest CT using multinational datasets. Nature communications, 11, 1, 1–7, Nature Publishing Group, 2020.

[10] Liang, Wenhua and Yao, Jianhua and Chen, Ailan and Lv, Qingquan and Zanin, Mark and Liu, Jun and Wong, SookSan and Li, Yimin and Lu, Jiatao and Liang, Hengrui and others. Early triage of critically ill Covid-19 patients using deep learning. Nature communications, 11, 1, 1–7, 2020.

[11] Kannan, Shantani and Subbaram, Kannan and Ali, Sheeza and Kannan, Hemalatha. The role of artificial intelligence and machine learning techniques: Race for Covid-19 vaccine. Archives of Clinical Infectious Diseases, 15, 2, Kowsar, 2020.

Interactive platform for evaluating scenarios and mathematical models applied to SarsCoV-2

The outbreak of infectious diseases, meaning, their appearance in regions not previously affected, requires the scientific community to produce knowledge on a large scale in order to apply measures for rapid control of the disease.

The dissemination of knowledge to the population becomes a crucial factor in the course of a pandemic, since strategies to control the pathogen depend on the entire population.

The importance of scientific dissemination becomes allied in the fight against the spread of the disease, becoming an indispensable tool as a guide for health managers and sanitarians.

Having this in mind, mathematical modeling in epidemiology stands out as a protagonist in the assessment of the dynamics of the disease and the reproduction of scenarios that envision alternatives for control.

In this newsletter we present the reasons for the importance of developing an Interactive Platform for evaluating scenarios and mathematical models applied to the new Sars-CoV2 coronavirus.

by ARTHUR RIOS, JULIANE OLIVEIRA, MORENO RODRIGUES, PABLO RAMOS

The epidemic of the new Covid-19 brought, without a doubt, a curious scenario. Thanks to the diversity of initiatives, we have access to a daily updated set of data containing information on confirmed and discarded cases, tests, occupation of hospital beds, and others. This information is made available on a time and space scale, providing analysis in monitoring the pandemic at aggregate levels by states or municipalities. This allows a large number of people to use this information in models, often not adequate, to build plots and, according to their interest, to disclose a certain scenario.

In this context, the proposal to develop an Interactive Platform for evaluating scenarios and mathematical models aims to create an environment that allows exploring these data as well as their use in different models, adjusted in real time to the data, such:

1. the user understands the limitations of the model,
2. use it correctly for scenario assessment, and
3. be able to compare the impact of the chosen model in the predicted scenario.

The proposal in question intends to offer, in a robust way, a tool that can be used by researchers, managers and others in such a way that they can:

• interact with the different type of data available in Brazil;
• evaluate the effect of measures taken on the epidemic curve of interest;
• making projections on short time scales (i.e. 7 - 10 days);
• verify the behavior of epidemic scenarios on long time scales (ie.> 100 days);
• and access metrics that assist in the decision-making process, such as the effective reproductive number, usually denoted by Rt , which estimates the average number of secondary infections that an individual, infected at time t, is able to generate.

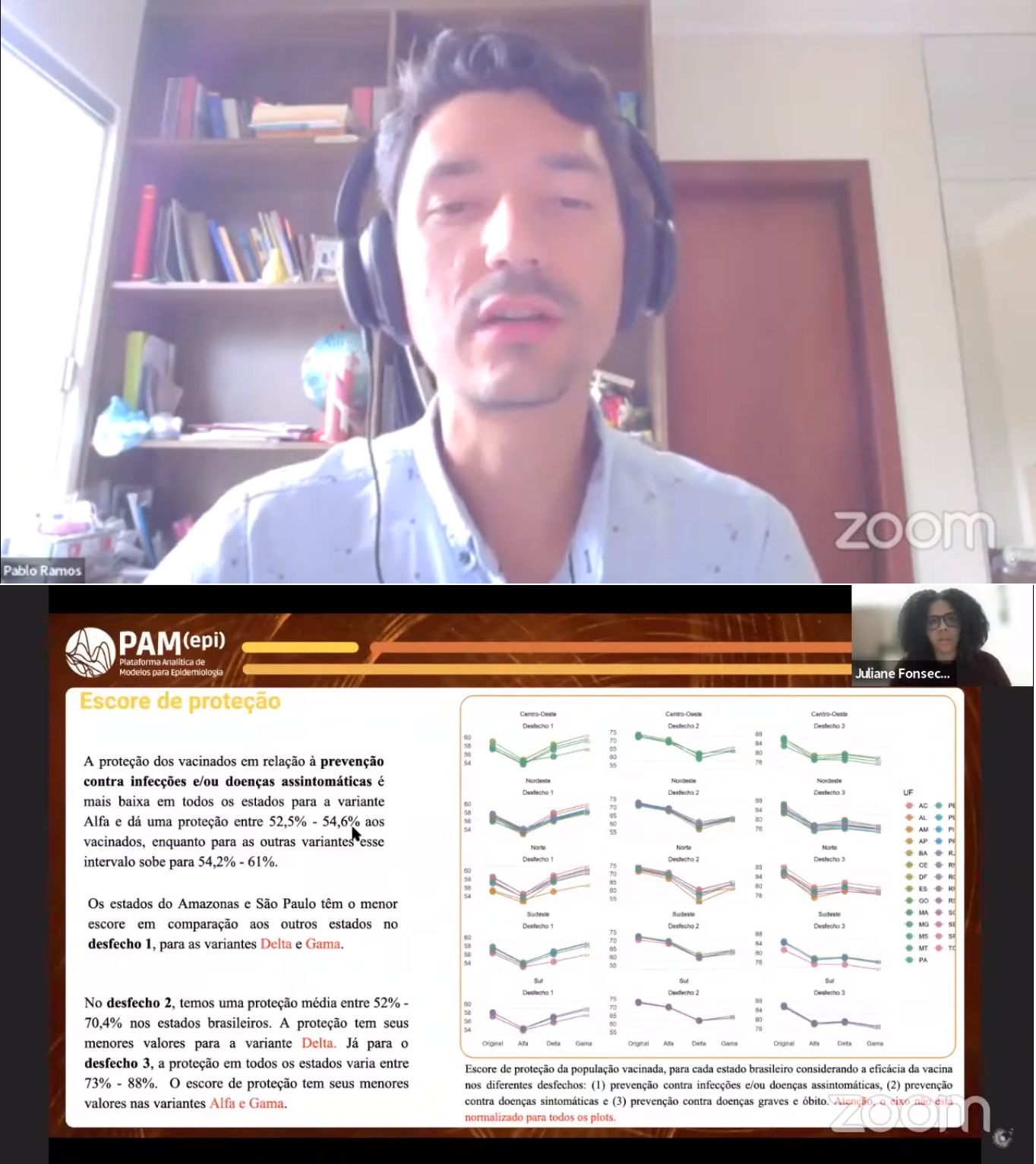
For the project's success, a Shinny platform containing the most frequent models used during the Covid-19 pandemic will be built. Concomitantly, a database containing the time series for each municipality in Brazil will be maintained based on data released at: https://brasil.io/dataset/covid19/caso/ - Ministry of Health and State Departments.

Before the modeling process, a set of rules will be created and the model will only be adjusted to the regions of interest that meet these assumptions. The results obtained for each model will be made available in the form of an interactive panel with a saving of dialog boxes, explaining how the information should be used as well as the main limitations or errors inherent to the process. The Platform will be built so that more models can be incorporated.